Advertisements
Advertisements
प्रश्न
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

उत्तर
Given in the question, in a parallelogram ABCD, P is a mid-point of BC such that ∠BAP = ∠DAP.
To prove that AD = 2CD
Proof: ABCD is a parallelogram
So, AD || BC and AB is transversal, then
∠A + ∠B = 180° ...[Sum of cointerior angles is 180°]
∠B = 180° – ∠A ...(i)
Now, in triangle ABP,
∠PAB + ∠B + ∠BPA = 180° ...[By angle sum property of a triangle]
`1/2 ∠A + 180^circ - ∠A + ∠BPA = 180^circ` ...[From equation (i)]
`∠BPA - (∠A)/2 = 0`
`∠BPA = (∠A)/2` ...(ii)
∠BPA = ∠BAP
AB = BP ...[Opposite sides of equal angles are equal]
In above equation multiplying both side by 2, we get
2AB = 2BP
2AB = BC ...[P is the mid-point of BC]
2CD = AD ...[ABCD is a parallelogram, then AB = CD and BC = AD]
APPEARS IN
संबंधित प्रश्न
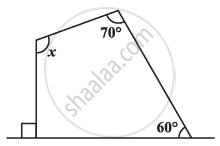
Find the angle measure x in the given Figure
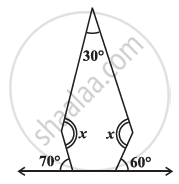
Find the angle measure x in the given Figure
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ.
In the given figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT = 152°, find x, y and z.

The figure formed by joining the mid-points of the adjacent sides of a square is a
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is ______.
The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a ______.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
