Advertisements
Advertisements
Question
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
Solution
Let the smallest angle be x
Then, the other angle is (3x - 24)
Now, x + 2x - 24 =180°
3x - 24 = 180°
⇒ 3x = 180 + 24
⇒ 3x = 204°
⇒ x = `204/3` = 68°
⇒ x = 68°
⇒ 2x - 24° = 2´68° - 24° =136° - 24° =112°
Hence four angles are 68°,112°, 68°,112°.
APPEARS IN
RELATED QUESTIONS
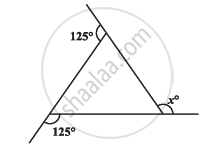
Find x in the following figure:
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
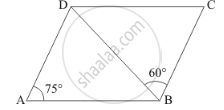
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13, then find the measure of the smallest angle.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
Sum of all the angles of a quadrilateral is 180°.
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
