Advertisements
Advertisements
Question
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
Solution
Let the measure of equal angles be x each.
Then, by the angle sum property of a quadrilateral, we have
x + x + x + 120° = 360°
⇒ 3x = 360° – 120°
⇒ 3x = 240°
⇒ x = 80°
APPEARS IN
RELATED QUESTIONS
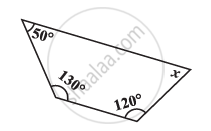
Find the angle measure x in the given Figure
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
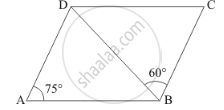
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
If PQRS is a square, then write the measure of ∠SRP.
If the angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13, then find the measure of the smallest angle.
The figure formed by joining the mid-points of the adjacent sides of a square is a
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
One angle of a quadrilateral is of 108º and the remaining three angles are equal. Find each of the three equal angles.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

The angles of a quadrilateral are in the ratio 1 : 2 : 3 : 4. The smallest angle is ______.
