Advertisements
Advertisements
प्रश्न
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
उत्तर
In quadrilateral DPBQ:
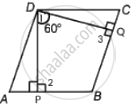
∠1 + ∠2 + ∠B + ∠3 = 360° ...[Angle sum property of quadrilateral]
60° + 90° + ∠B + 90° = 360°
∠B + 240° = 360°
∠B = 360° – 240°
∠B = 120°
Since, ∠ADC = ∠B = 120° ...[Opposite angles of a parallelogram are equal]
∠A + ∠B = 180° ...[Sum of consecutive interior angle is 180°]
∠A + 120° = 180°
∠A = 180° – 120°
∠A = 60°
So, ∠C = ∠A = 60° ...[Opposite angle of a parallelogram are equal]
APPEARS IN
संबंधित प्रश्न
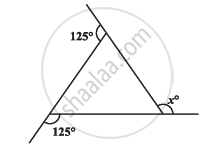
Find x in the following figure:
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram .
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
Diagonals necessarily bisect opposite angles in a
The figure formed by joining the mid-points of the adjacent sides of a square is a
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Which of the following can be four interior angles of a quadrilateral?
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
