Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
उत्तर
The quadrilateral can be drawn as follows:
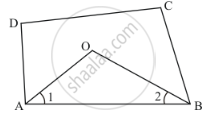
We have AO and BO as the bisectors of angles ∠A and ∠B respectively.
In ΔAOB,We have,
∠AOB + ∠1 +∠2 = 180°
∠AOB = 180° -(∠1 +∠2 )
∠AOB = 180° -`(1/2∠A + 1/2 ∠B)`
∠AOB = 180° - `1/2(∠A +∠B)` …… (1)
By angle sum property of a quadrilateral, we have:
∠A + ∠B +∠C + ∠D = 360°
∠A+ ∠B = 360° -(∠C +∠D)
Putting in equation (1):
`∠AOB =180° - 1/2[360° - (∠C + ∠D )]`
`∠AOB = 180° - 180° +(∠C +∠D)/2]`
`∠AOB = 1/2 (∠C +∠D)` ……(2)
It is given that ∠AOB = 75° in equation (2), we get:
`75° = 1/2 (∠C +∠D)`
`1/2(∠C+∠D) = 75°`
∠C + ∠D = 150°
Hence, the sum of ∠Cand ∠D is 150°.
APPEARS IN
संबंधित प्रश्न
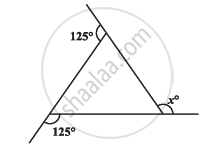
Find x in the following figure:
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13 Find all the angles of the quadrilateral.
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
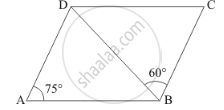
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
The two diagonals are equal in a
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
Can the angles 110º, 80º, 70º and 95º be the angles of a quadrilateral? Why or why not?
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Which of the following can be four interior angles of a quadrilateral?
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
