Advertisements
Advertisements
प्रश्न
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
उत्तर
The rectangle ABCD is given as:
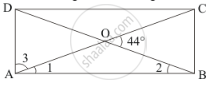
We have,
∠BOC +∠BOA = 180° (Linear pair)
44° +∠BOA = 180°
∠BOA = 180° -44°
∠BOA = 136°
Since, diagonals of a rectangle are equal and they bisect each other. Therefore, in ΔOAB, we have
OA = OB (Angles opposite to equal sides are equal.)
Therefore,
∠1 = ∠2
Now,in ΔOAB, we have
∠BOA + ∠1 +∠2 = 180
∠BOA + 2∠1 = 180°
2∠1 = 44°
∠1 = 22°
Since, each angle of a rectangle is a right angle.
Therefore,
∠BAD = 90°
∠1+∠3 = 90°
22° +∠3 = 90°
∠3 = 68°
Thus, ∠OAD = 68°
Hence, the measure of∠OAD is 68°.
APPEARS IN
संबंधित प्रश्न
Find the angle measure x in the given Figure
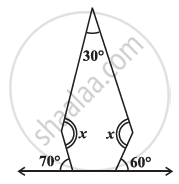
Find the angle measure x in the given Figure
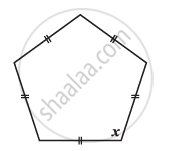
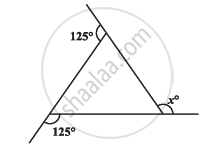
Find x in the following figure:
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
Diagonals necessarily bisect opposite angles in a
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
The sum of all ______ of a quadrilateral is 360°.
Sum of all the angles of a quadrilateral is 180°.
