Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13 Find all the angles of the quadrilateral.
рдЙрддреНрддрд░
Let the common ratio between the angle is ‘ЁЭСе’ so the angles will be 3x, 5x, 9x and 13x
respectively
Since the sum of all interior angles of a quadrilateral is 360°
∴ 3x + 5x + 9x +13x = 360°
⇒ 30x = 360°
⇒ x =12°
Hence, the angles are
3x = 3 × 12 = 36°
5x = 5 × 12 = 60°
9x = 9 ×12 =108°
13x =13× 12 =156°
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
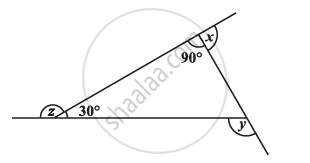
Find x + y + z
Find x + y + z + w
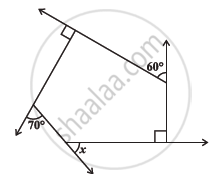
Find x in the following figures.
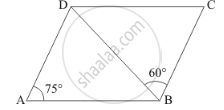
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.
A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is ______.
Sum of all the angles of a quadrilateral is 180°.
Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
