Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
उत्तर
In ΔDOC
`∠`1+ `∠`COD + `∠`2 =180° [Angle sum property of a triangle]
⇒ `∠`COD = 180 - `∠`1- `∠`2
⇒ `∠`COD =180 - `∠`1+ `∠`2
⇒ `∠`COD = 180- `[1/2∠c+1/2∠d]`
[ ∵ OC and OD are bisectors of `∠`C and `∠`D represents ]
⇒ `∠`COD = 180-`1/2` (`∠`C and `∠`D)] ............1
In quadrilateral ABCD
`∠`A + `∠`B + `∠`C + `∠`D = 360°
`∠`C + `∠`D = 360 - `∠`A + `∠`B ..............(2) [ Angle sum property of quadrilateral]
Substituting (ii) in (i)
⇒ `∠`COD = 180 -`1/2`(360 - `∠`A + `∠`B ))
⇒ `∠`COD = 180 -180 +`1/2`(`∠`A +`∠`B )
⇒ `∠`COD =`1/2`(`∠`A +`∠`B )
APPEARS IN
संबंधित प्रश्न
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
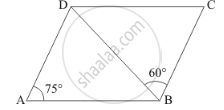
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
If PQRS is a square, then write the measure of ∠SRP.
In a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB = 75°, then write the value of ∠C + ∠D.
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
Diagonals necessarily bisect opposite angles in a
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
In a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
