Advertisements
Advertisements
प्रश्न
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram .
उत्तर
Let the measure of the angle be x
∴ The measure of the angle adjacent is `(2x)/3`
We know that the adjacent angle of a parallelogram is supplementary
Hence x + `(2x) / 3` = 180°
2x + 3x = 540°
⇒ 5x = 540°
⇒ x = 108°
Adjacent angles are supplementary
⇒ x +108° = 180°
⇒ x =180° -108° = 72°
⇒ x = 72°
Hence, four angles are : 180°, 72°,108°, 72°
APPEARS IN
संबंधित प्रश्न
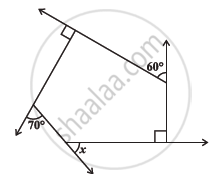
Find x in the following figures.
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
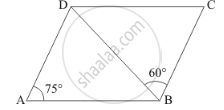
In Fig. below, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute
∠CDB and ∠ADB.
In the given figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD = 146°, find ∠AOB.
If the degree measures of the angles of quadrilateral are 4x, 7x, 9x and 10x, what is the sum of the measures of the smallest angle and largest angle?
Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.
Can all the angles of a quadrilateral be right angles? Give reason for your answer.
In the following figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

Sum of all the angles of a quadrilateral is 180°.
