Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measure of each angles of the quadrilateral
उत्तर
Let the angles of the quadrilateral be
A = x, B = 2x, C = 4x and D = 5x then,
A + B + C + D = 360°
⇒ x + 2x + 4x + 5x = 360°
⇒ 12x = 360°
⇒ x = `(360°)/12`
⇒ x = 30°
∴ A = x = 30°
B = 2x = 60°
C = 4x = 30° (4) = 120°
D = 5x = 5 (30°) = 150°
APPEARS IN
संबंधित प्रश्न
Find the angle measure x in the given Figure
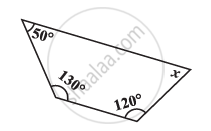
Find the angle measure x in the given Figure
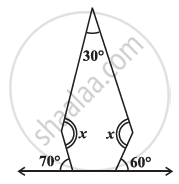
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle
In a quadrilateral ABCD, CO and DO are the bisectors of `∠`C and ∠D respectively. Prove that
`∠`COD = `1/2` (`∠`A+ `∠`B).
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D .
The diagonals of a rectangle ABCD meet at O, If ∠BOC = 44°, find ∠OAD.
Diagonals necessarily bisect opposite angles in a
The two diagonals are equal in a
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
