Advertisements
Advertisements
प्रश्न
ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
उत्तर
Let sides of a rhombus be AB = BC = CD = DA = x
Now, join DB.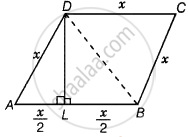
In ΔALD and ΔBLD,
∠DLA = ∠DLB = 90°
AL = BL = `x/2` ...[Since, DL is a perpendicular bisector of AB]
And DL = DL ...[Common side]
∴ ΔALD ≅ ΔBLD ...[By SAS congruence rule]
AD = BD ...[By CPCT]
Now, in ΔADB,
Then, ΔADB is an equilateral triangle.
∴ ∠A = ∠ADB = ∠ABD = 60°
Similarly, ΔDBC is an equilateral triangle.
∴ ∠C = ∠BDC = ∠DBC = 60°
Also, ∠A = ∠C
∴ ∠D = ∠B = 180° – 60° = 120° ...[Since, sum of interior angles is 180°]
APPEARS IN
संबंधित प्रश्न
`square`ABCD is a parallelogram, P and Q are midpoints of side AB and DC respectively, then prove `square`APCQ is a parallelogram.

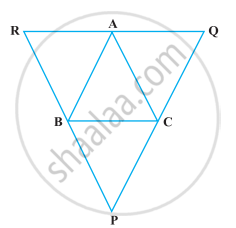
Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ∆ABC as shown in the following figure. Show that BC = `1/2` QR.
A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.
