Advertisements
Advertisements
प्रश्न
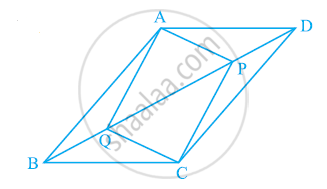
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
उत्तर
(i) In ΔAPD and ΔCQB,
∠ADP = ∠CBQ ...(Alternate interior angles for BC || AD)
AD = CB ...(Opposite sides of parallelogram ABCD)
DP = BQ ...(Given)
∴ ΔAPD ≅ ΔCQB ...(Using SAS congruence rule)
(ii) As we had observed that ΔAPD ≅ ΔCQB,
∴ AP = CQ ...(CPCT)
(iii) In ΔAQB and ΔCPD,
∠ABQ = ∠CDP ...(Alternate interior angles for AB || CD)
AB = CD ...(Opposite sides of parallelogram ABCD)
BQ = DP ...(Given)
∴ ΔAQB ≅ ΔCPD ...(Using SAS congruence rule)
(iv) As we had observed that ΔAQB ≅ ΔCPD,
∴ AQ = CP ...(CPCT)
(v) From the results obtained in (ii) and (iv),
AQ = CP and
AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
Every parallelogram is a rhombus.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.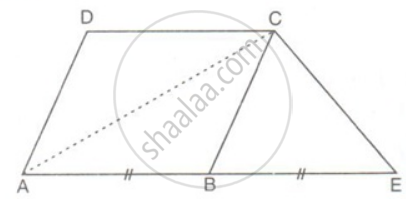
In the given figure, ABC is a triangle and AD is the median.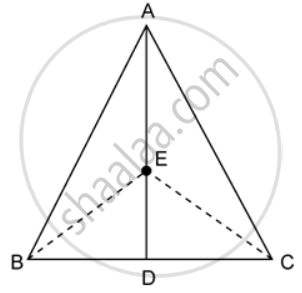
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
The opposite sides of a rectangle are equal in length.
Give reason for the following :
A square can be thought of as a special rectangle.
