Advertisements
Advertisements
Question
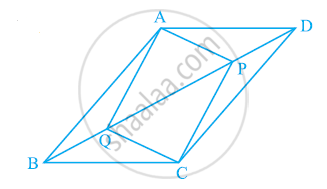
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
Solution
(i) In ΔAPD and ΔCQB,
∠ADP = ∠CBQ ...(Alternate interior angles for BC || AD)
AD = CB ...(Opposite sides of parallelogram ABCD)
DP = BQ ...(Given)
∴ ΔAPD ≅ ΔCQB ...(Using SAS congruence rule)
(ii) As we had observed that ΔAPD ≅ ΔCQB,
∴ AP = CQ ...(CPCT)
(iii) In ΔAQB and ΔCPD,
∠ABQ = ∠CDP ...(Alternate interior angles for AB || CD)
AB = CD ...(Opposite sides of parallelogram ABCD)
BQ = DP ...(Given)
∴ ΔAQB ≅ ΔCPD ...(Using SAS congruence rule)
(iv) As we had observed that ΔAQB ≅ ΔCPD,
∴ AQ = CP ...(CPCT)
(v) From the results obtained in (ii) and (iv),
AQ = CP and
AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.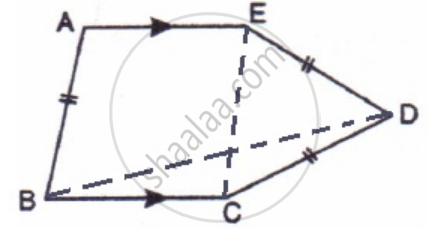
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.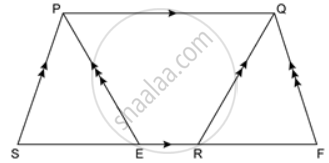
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
In the given figure, ABC is a triangle and AD is the median.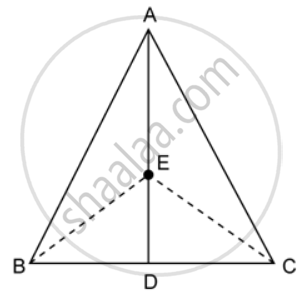
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
