Advertisements
Chapters
![NCERT solutions for Mathematics [English] Class 9 chapter 8 - Quadrilaterals - Shaalaa.com](/images/mathematics-english-class-9_6:e75a1668572245b2974a4e6dc62140a3.jpg "NCERT solutions for Mathematics [English] Class 9 chapter 8 - Quadrilaterals")
Advertisements
Solutions for Chapter 8: Quadrilaterals
Below listed, you can find solutions for Chapter 8 of CBSE NCERT for Mathematics [English] Class 9.
NCERT solutions for Mathematics [English] Class 9 8 Quadrilaterals EXERCISE 8.1 [Pages 110 - 111]
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show that the diagonals of a square are equal and bisect each other at right angles.
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
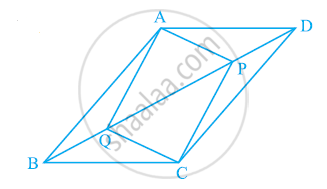
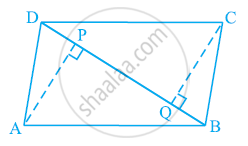
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
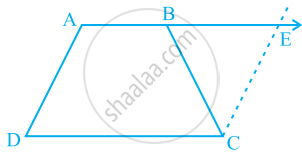
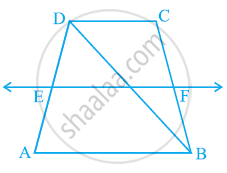
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
NCERT solutions for Mathematics [English] Class 9 8 Quadrilaterals EXERCISE 8.2 [Pages 113 - 114]
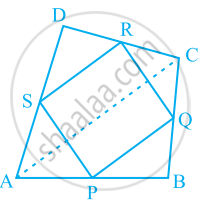
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
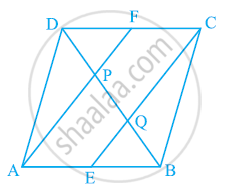
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
Solutions for 8: Quadrilaterals
NCERT solutions for Mathematics [English] Class 9 chapter 8 - Quadrilaterals
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT solutions for Mathematics Mathematics [English] Class 9 CBSE 8 (Quadrilaterals) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 8 Quadrilaterals are Concept of Quadrilaterals, Properties of a Quadrilateral, Types of Quadrilaterals, Theorem of Midpoints of Two Sides of a Triangle, Property: The Opposite Sides of a Parallelogram Are of Equal Length., Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles., Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram., Property: The Opposite Angles of a Parallelogram Are of Equal Measure., Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram., Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection), Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram, Another Condition for a Quadrilateral to Be a Parallelogram, Concept of Quadrilaterals, Properties of a Quadrilateral, Types of Quadrilaterals, Theorem of Midpoints of Two Sides of a Triangle, Property: The Opposite Sides of a Parallelogram Are of Equal Length., Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles., Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram., Property: The Opposite Angles of a Parallelogram Are of Equal Measure., Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram., Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection), Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram, Another Condition for a Quadrilateral to Be a Parallelogram.
Using NCERT Mathematics [English] Class 9 solutions Quadrilaterals exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer NCERT Textbook Solutions to score more in exams.
Get the free view of Chapter 8, Quadrilaterals Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
