Advertisements
Advertisements
Question
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution
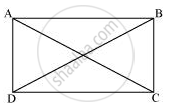
Let ABCD be a parallelogram. To show that ABCD is a rectangle, we must prove that one of its interior angles is 90°.
In ΔABC and ΔDCB,
AB = DC ...(Opposite sides of a parallelogram are equal)
BC = BC ...(Common)
AC = DB ...(Given)
∴ ΔABC ≅ ΔDCB ...(By SSS Congruence rule)
⇒ ∠ABC = ∠DCB
It is known that the sum of the measures of angles on the same side of transversal is 180°.
∠ABC + ∠DCB = 180° ...(AB || CD)
⇒ ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
Since ABCD is a parallelogram and one of its interior angles is 90°, ABCD is a rectangle.
APPEARS IN
RELATED QUESTIONS
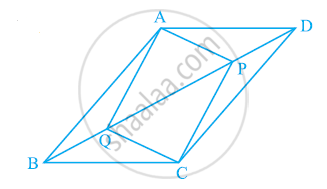
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
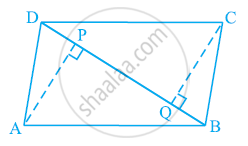
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
Prove that the median of a triangle divides it into two triangles of equal area.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
