Advertisements
Advertisements
Question
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Solution
The sides and diagonal of a square form a right triangle as each angle of a square is a right angle.
Diagonal is the side opposite to the right angle, therefore it is the hypotenuse
Here, Diagonal of the square = `12sqrt(2)"cm"`
Let the side of the square = s
∴ `sqrt("s"^2 + "s"^2) = 12sqrt(2)`
⇒ `sqrt(2"s"^2) = 12sqrt(2)`
⇒ `"s"sqrt(2) = 12sqrt(2)`
⇒ s = 12
We know,
The area of a square with side s = s2
∴ s2
= (12)2
= 144cm2.
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
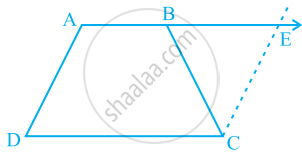
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN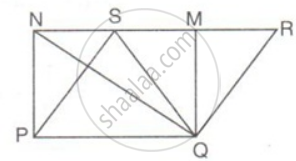
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.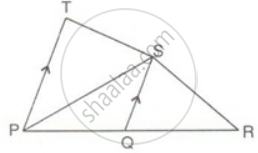
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.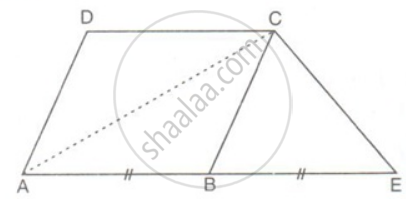
Find the area of each of the following figure: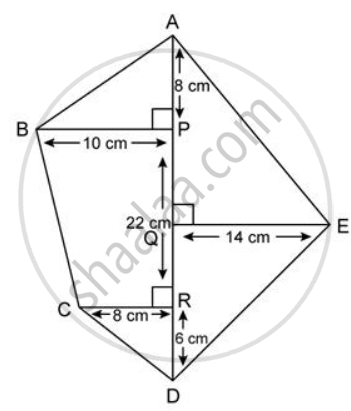
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
The opposite sides of a rectangle are equal in length.
All the sides of a rhombus are of equal length.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
