Advertisements
Advertisements
Question
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN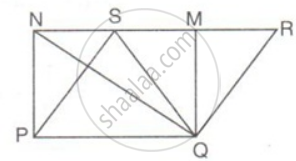
Solution
(i) Area of a rectangle and area of a parallelogram on the same base is equal.
Here,
For rectangle PQMN, base = PQ
For parallelogram PQRS, base = PQ
Therefore, Area of rectangle PQMN = Area of parallelogram PQRS
Area of rectangle PQMN = 84cm2
(ii) ar(ΔPQS) = `(1)/(2)` x ar(parallelogram PQRS)
ar(ΔPQS) = `(1)/(2) xx 84"cm"^2`
ar(ΔPQS) = 42cm2
(iii) ar(ΔPQN) = `(1)/(2)` x ar(rectangle PQMN)
ar(ΔPQN) = `(1)/(2) xx 84"cm"^2`
ar(ΔPQN) = 42cm2.
APPEARS IN
RELATED QUESTIONS
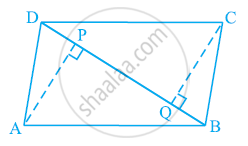
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
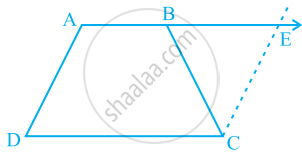
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.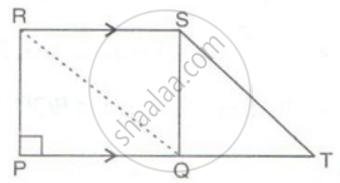
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.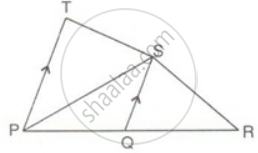
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
All the sides of a parallelogram are of equal length.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Give reasons for the following :
A square can be thought of as a special rhombus.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

