Advertisements
Advertisements
Question
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Solution
Let the side of the smaller square = x
∴ the side of the larger square = x + 4
We know, The area of a square with side s = s2
∴ The area of a square with side x = x2
and, The area of a square with side x + 4 = (x + 4)2
Now, the sum of the two area = 400
⇒ x2 + (x+ 4)2 = 400
⇒ x2 + x2 + 16 + 8x = 400
⇒ 2x2 + 8x + 16 = 400
⇒ 2(x2 + 4x + 8) = 2(200)
⇒ x2 + 4x + 8 = 200
⇒ x2 + 4x - 192 = 0
Splittting the middle term, we have
x2 + 16x - 12x - 192 = 0
⇒ x(x + 16) - 12(x + 16) = 0
⇒ (x + 16)(x - 12) = 0
⇒ x = -16, x = 12
But x is the length of the side of a square,
∴ x ≠ -16
∴ x = 12
⇒ the side ofthe smaller square = 12cm
∴ the side of the larger square
= 12 + 4
= 16cm.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.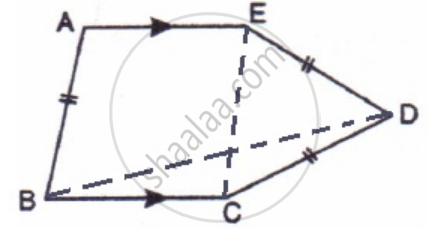
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.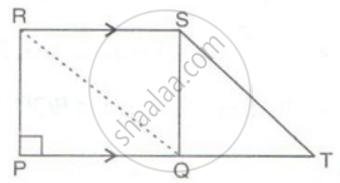
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure: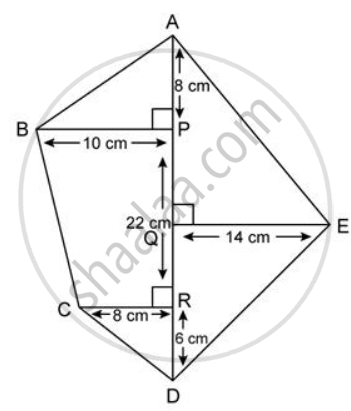
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
The diagonals of a square are perpendicular to one another.
All the sides of a parallelogram are of equal length.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Square is also a parallelogram.
