Advertisements
Advertisements
Question
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.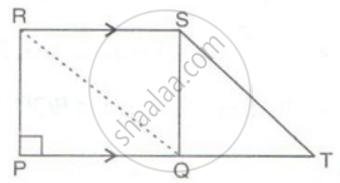
Solution
(i) ar(ΔQTS) = `(1)/(2)` x ar(parallelogram QTSR)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
⇒ ar(parallelogram QTSR) = 2 x ar(ΔQTS)
⇒ ar(parallelogram QTSR) = 2 x 60cm2
⇒ ar(parallelogram QTSR) = 120cm2
(ii) ar(ΔQTS) = `(1)/(2)` x ar(parallelogram QTSR)
ar(ΔQTS) = ar(ΔRSQ) = 60cm2
Now,
ar(ΔRSQ) = `(1)/(2)` x ar(rectangle PQRS)
⇒ ar(rectangle PQRS) = 2 x ar(ΔRSQ)
⇒ ar(rectangle PQRS) = 2 x 60cm2
⇒ ar(rectangle PQRS) = 120cm2
(iii) Since PQRS is a rectangle,
Therefore RS = PQ .....(i)
QTSR is a parallelogram,
Therefore, RS = QT .....(ii)
From (i) and (ii)
PQ = QT .......(iii)
In ΔPSQ and ΔQST
QS = QS
PQ = QT ...(from (iii))
∠PQS = ∠SQT = 90°
Therefore, ΔPSQ ≅ ΔQST
Area of two congruent triangles is equal.
Hence, ar(ΔPSQ) = ar(ΔQTS) = 60cm2.
APPEARS IN
RELATED QUESTIONS
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.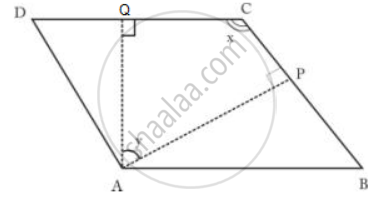
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.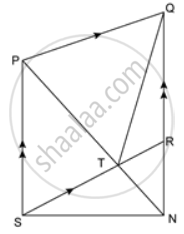
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.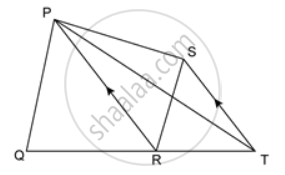
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.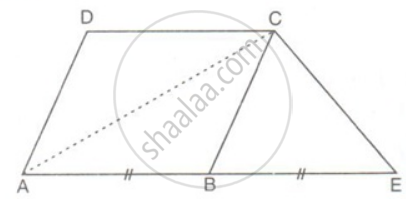
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
All the sides of a rhombus are of equal length.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
