Advertisements
Advertisements
Question
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
Solution

(i) Let ∠POC = x°.
We know that,
Each interior angle equals to 90°. Diagonals of square bisect the interior angles.
From figure,
⇒ ∠OCP = ∠OBP = `(90°)/2` = 45°.
We know that,
In a triangle, an exterior angle is equal to sum of two opposite interior angles.
∴ ∠OPB = ∠OCP + ∠POC
⇒ ∠OPB = 45° + x° ...(1)
In △OBP,
⇒ OB = BP ...(Given)
⇒ ∠OPB = ∠BOP (Angles opposite to equal sides are equal) ...(2)
From equation (1) and (2), we get:
⇒ ∠BOP = 45° + x° ...(3)
We know that,
Diagonals of square are perpendicular to each other.
∴ ∠BOC = 90°
⇒ ∠BOP + ∠POC = 90°
⇒ 45° + x° + x° = 90°
⇒ 2x° = 90° - 45°
⇒ 2x° = 45°
⇒ x° = `(45°)/2`
⇒ x° = `(22 1/2)^°`
⇒ ∠POC = `(22 1/2)^°`
Hence, proved that ∠POC = `(22 1/2)^°`
(ii) From figure,
⇒ ∠BDC = 45° ...(Diagonals of a square bisect the interior angles)
⇒ ∠BDC = 2 × `(22 1/2)^°`
⇒ ∠BDC = 2 × ∠POC
⇒ ∠BDC = 2 ∠POC
Hence, proved that ∠BDC = 2 ∠POC.
(iii) From equation (3),
⇒ ∠BOP = 45° + x°
⇒ ∠BOP = 45° + 22.5°
⇒ ∠BOP = 67.5°
⇒ ∠BOP = 3 × 22.5°
⇒ ∠BOP = 3 × ∠POC
⇒ ∠BOP = 3 ∠POC
Hence, proved that ∠BOP = 3 ∠COP.
APPEARS IN
RELATED QUESTIONS
Show that the diagonals of a square are equal and bisect each other at right angles.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.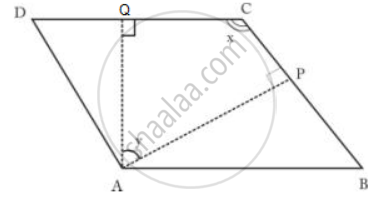
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the given figure, ABC is a triangle and AD is the median.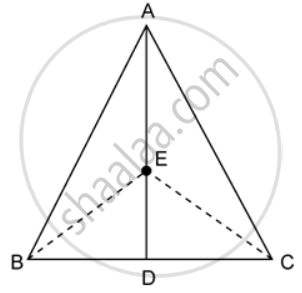
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
All the sides of a rhombus are of equal length.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
