Advertisements
Advertisements
Question
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.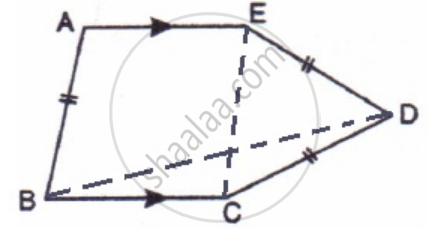
Solution
In the given figure
Given that AE = BC
We have to find ∠AEC and ∠BCD
In the quadrilateral AECB
(AE = BC and AE || BC)
So quadrilateral is a parallelogram
⇒ ∠BAE + ∠AEC = 180°
⇒ 102° + ∠AEC = 180°
⇒ ∠AEC = 78°
Also, ∠BAE = ∠BCE = 102°
AB = EC (because AECB is a parallelogram )
Now consider ΔECD
EC = ED = CD [Since AB = EC ]
Therefore ΔEDC is an equilateral triangle.
⇒ ∠ECD = 60°
∠BCD = ∠BCE + ∠ECD
⇒ ∠BCD = 102° + 60°
⇒ ∠BCD = 162°
Therefore ∠AEC = 78° and ∠BCD = 162°
APPEARS IN
RELATED QUESTIONS
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.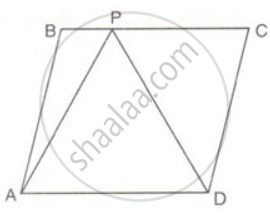
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN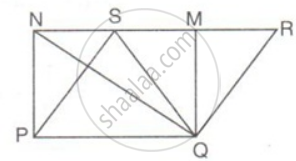
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Name polygon.
Make two more examples of this.
Name polygon.

Make two more examples of this.
