Advertisements
Advertisements
Question
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Solution
The length of the rectangle = x m
Let the breadth of the rectangle = b m
The perimeter of a rectangle with length l and breadth b = P = 2(l + b)
The perimeter of a triangle with length x and breadth b = 2(x + b) = 300
⇒ (x + b) = 150
⇒ b = 150 - x
The area of a rectangle with length l and breadth b = A = l x b
The area of a rectangle with length x and breadth (150 - x)
= X x (150 - x)
= 5600
⇒150x - x2 = 5600
⇒ x2 - 150x + 5600 = 0
⇒ x2 - 80x - 70x + 5600 = 0
⇒ x(x - 80) - 70(x - 80) = 0
⇒ (x - 80)(x - 70) = 0
⇒ x = 70m, 80m
When breadth = 70m, then the length
= 150 - 70
= 80m
When breadth = 80m, then the length
= 150 - 80
= 70m.
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.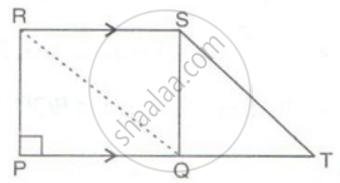
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.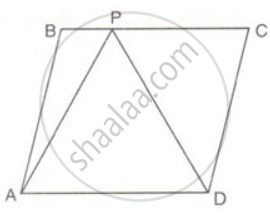
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN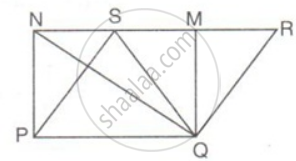
Prove that the median of a triangle divides it into two triangles of equal area.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, ABC is a triangle and AD is the median.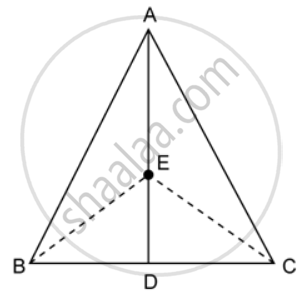
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of each of the following figure:
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
