Advertisements
Advertisements
Question
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
Solution
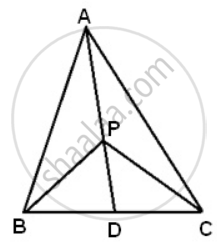
AD is the median of ΔABC, so, it will divide ΔABC into two triangles of equal areas.
Therefore, Area(ΔABD) = area(ΔACD) ...(1)
Now PD is the median of ΔPBC.
Therefore, Area(ΔPBD) = area(ΔPCD) ...(2)
Subtract equation (2) from equation (1), we have
Area(ΔABD) - area(ΔPBD) = Area(ΔACD) - Area(ΔPCD)
Area(ΔABP) = area(ΔACP).
APPEARS IN
RELATED QUESTIONS
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.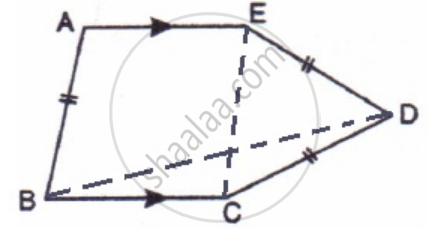
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.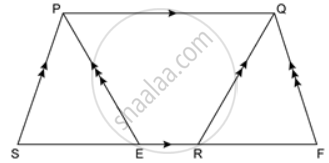
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.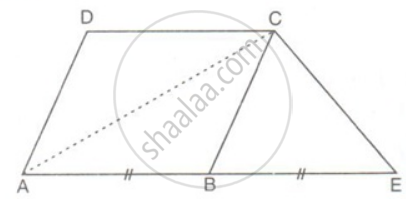
Find the area of each of the following figure: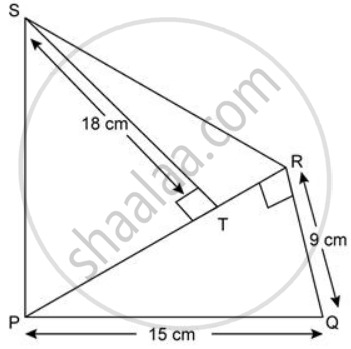
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
The diagonals of a square are perpendicular to one another.
All the sides of a rhombus are of equal length.
Give reason for the following :
A square can be thought of as a special rectangle.
Examine whether the following is a polygon. If it is not, say why?
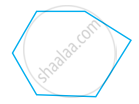
Name polygon.
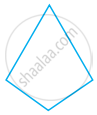
Make two more examples of this.
