Advertisements
Advertisements
Question
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
Solution
Let the breadth of the rectangle = xm
The area of a rectangle with length l and breadth b = A = l x b
∴ The area of a rectangle with length 240m and breadth xm = A = 240x
⇒ 240x = 36000
⇒ x = `(36000)/(240)`
= 150m
Now, the perimeter of a rectangle with length l and breadth b = P = 2(l + b)
∴ The perimeter of a rectangle with length 240 and breadth 150 is
P = 2(240 + 150)
= 2(390)
= 780
The cost of fencing 1m = Rs.2.50
⇒ The cost of fencing 780m
= Rs.2.50 x 780
= Rs.1950.
APPEARS IN
RELATED QUESTIONS
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.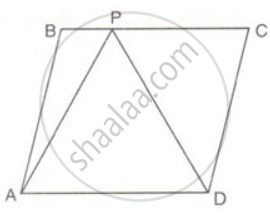
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
The diagonals of a square are perpendicular to one another.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Square is also a parallelogram.
