Advertisements
Advertisements
Question
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
Solution
The perimeter of a square with side s = p = 4s
∴ Here, the perimeter of the square are 128cm and 96cm
∴ the sides of the two squares are 32cm and 24cm
We know, The area of a square with side s = s2
∴ the areas of the two squares are = 32cm2 = 1024cm2 and 24cm2 = 576cm2
∴ the combined area
= area of the new square
= 1024cm2 + 576cm2
= 1600cm2
the side of the square
= `sqrt(1600)`
= 40cm
The perimeter of a square with side 40
= 4 x 40
= 160cm
The sides and diagonal of a square from a right triangle as each angle of a square is a right angle.
Diagonal is the side opposite to the right angle, therefore it is the hypotenuse
Here, diagonal of the square
= `sqrt(40^2 + 40^2)`
= `40sqrt(2)`
= 40(1.414)
= 56.57cm.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the following figures, ABCD is a parallelogram.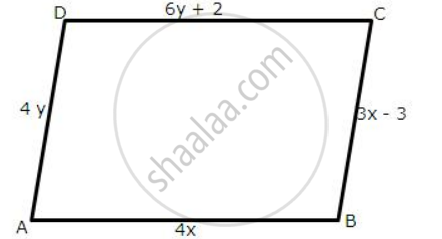
find the values of x and y.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.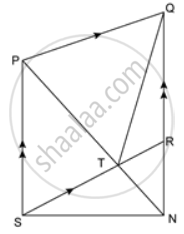
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
