Advertisements
Advertisements
Question
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.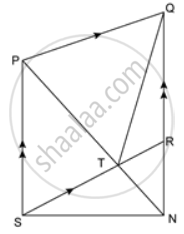
Solution
ΔPQT and parallelogram PQRS are on the same base PQ and between the same parallel lines PQ and SR.
∴ Δ(ΔPQT) = `(1)/(2)"A"`(parallelogram PQRS) ....(i)
ΔPSN and parallelogram PQRS are on the same base PS and between the same parallel lines PS and QN.
∴ Δ(ΔPSN) = `(1)/(2)"A"`(parallelogram PQRS) ....(ii)
Adding equations (i) and (ii), we get
∴ A(ΔPQT) + A(ΔPSN) = A(parallelogram PQRS)
⇒ A(quad. PSNQ) - A(ΔQTN) = A(parallelogram PQRS)
⇒ A(quad. PSNQ) - A(ΔQTN) = A(quad. PSNQ) - A(ΔSRN)
⇒ A(ΔQTN = A(ΔSRN)
Subtracting A(ΔRTN) from both the sides, we get
A(ΔQTN) - A(ΔRTN) = A(ΔSRn) - A(ΔRTN)
⇒ A(ΔQTR) = A(ΔSTN).
APPEARS IN
RELATED QUESTIONS
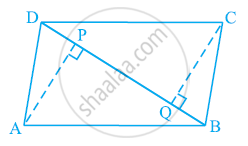
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
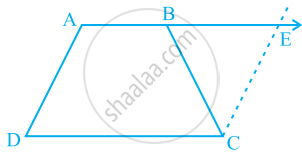
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
Prove that the median of a triangle divides it into two triangles of equal area.
In the given figure, ABC is a triangle and AD is the median.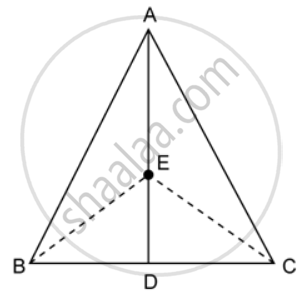
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Each angle of a rectangle is a right angle.
The diagonals of a square are perpendicular to one another.
All the sides of a rhombus are of equal length.
Give reason for the following :
A square can be thought of as a special rectangle.
Examine whether the following is a polygon. If it is not, say why?

