Advertisements
Advertisements
Question
In the given figure, ABC is a triangle and AD is the median.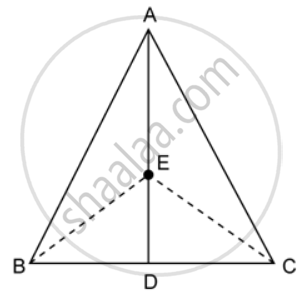
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Solution
AD is the median of ΔABC.
Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area(ΔABD) = Area(ΔACD) ….(i)
Similarly, ED is the median of ΔEBC.
∴ Area(DEBD) = Area(DECD) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔABD) - Area(ΔEBD) = Area(ΔACD) - Area(ΔECD)
⇒ Area(ΔABE) = Area(ΔACE).
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
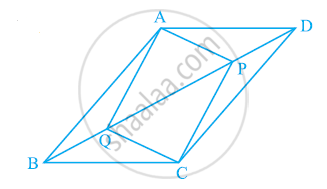
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.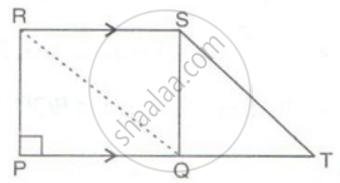
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.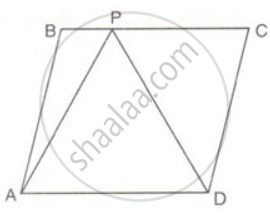
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
