Advertisements
Advertisements
Question
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
Solution
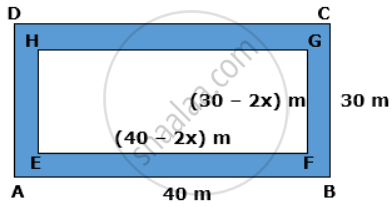
Let the given rectangular field be ABCD with length AB = 40m and width BC = 30m.
If the width of uniform path = x m,
the length of rectangle excluding path is EF = (40 - 2x) m and the width of rectangle excluding path is FG = (30 - 2x) m.
Now,
Area of rectangle ABCD -Area of rectangle EFGH = Area of path
⇒ (40 x 30) - [(40 - 2x) x (30 - 2x)] = 136
⇒ 1200 - [200 - 80x - 60x + 4x2] = 136
⇒ 1200 - 1200 + 140x - 4x2 = 136
⇒ 4x2 - 140x + 136 = 0
⇒ x2 - 35x + 34 = 0
⇒ x2 - 34x - x + 34 = 0
⇒ x(x - 34) -1(x - 34) = 0
⇒ (x - 34)(x - 1) = 0
⇒ x = 34 or x = 1
Rejected x = 34 (because it does not satisfy the calculation of the area of the path i.e. 136m2), we get x = 1
Thus, the width of the path is 1m.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.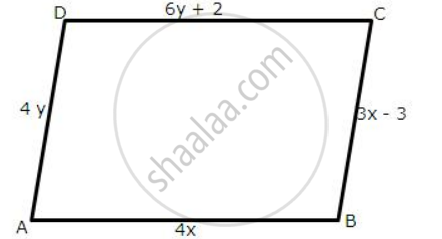
find the values of x and y.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.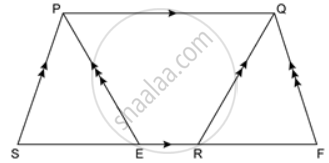
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.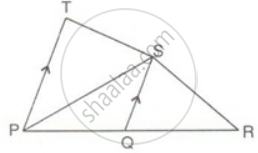
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
The opposite sides of a trapezium are parallel.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?
Examine whether the following is a polygon. If it is not, say why?

