Advertisements
Advertisements
Question
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Solution
Area of grassy plot
= 38 x 14
= 532m2
Length of a grass plot with footpath = 38 + 2 = 40m
Width of a grass plot with footpath = 14 + 2 = 16m
∴ Area of the grass plot with footpath = 40 x 16 = 640m2
Area of the footpath = Area of the grass plot with footpath - Area of grassy plot
= (640 - 532)m2
= 180m2
= 1080000m2
Area of each title = 625cm2
∴ Number of titles
= `"Area of the footpath"/"Area of each title"`
= `(1080000)/(625)`
= 1728.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.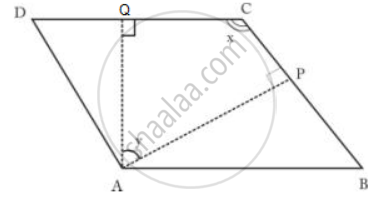
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.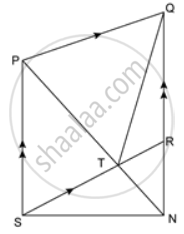
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.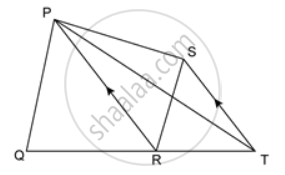
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.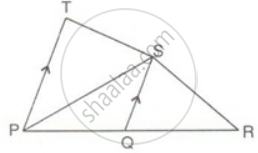
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.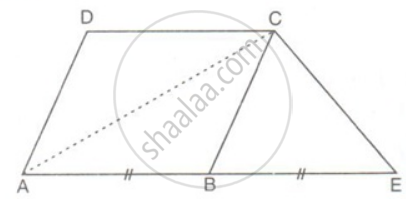
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
The opposite sides of a rectangle are equal in length.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.
Make two more examples of this.
