Advertisements
Advertisements
Question
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
Solution
In the figure, ABCD is a parallelogram
∠D = ∠B ...[Since opposite angles are equal.]
6x + 3y - 8 = 7y
6x + 3y - 7y = 8
6x - 4y = 8
2(3x - 2y) = 8
3x - 2y = 4 ...(i)
∠A + ∠B = 180°
4x + 20° + 7y = 180°
4x + 7y = 160° ...(ii)
Multiply by equation (i) × 4 and equation (ii) × 3
12x - 8y = 16
12x + 21y = 480
- - -
- 29y = - 464
y = `(- 464)/(- 29)`
y = 16
Put y = 16 in equation (i)
∴ 3x - 2y = 4
⇒ 3x - 2(16) = 4
⇒ 3x - 32 = 4
⇒ 3x = 4 + 32
⇒ 3x = 36
⇒ x = `36/3`
⇒ x = 12
APPEARS IN
RELATED QUESTIONS
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

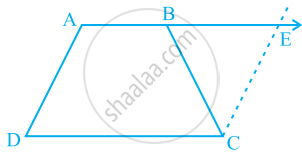
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
State, 'true' or 'false'
Diagonals of a rhombus are equal.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN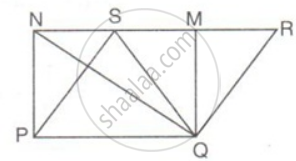
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.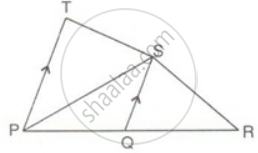
Prove that the median of a triangle divides it into two triangles of equal area.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Each angle of a rectangle is a right angle.
The opposite sides of a rectangle are equal in length.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reason for the following :
Square is also a parallelogram.
