Advertisements
Advertisements
Question
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

Solution
(i) ABCD is a parallelogram.
∴ ∠DAC = ∠BCA ...(Alternate interior angles) ...(1)
And, ∠BAC = ∠DCA ...(Alternate interior angles) ...(2)
However, it is given that AC bisects ∠A.
∴ ∠DAC = ∠BAC ...(3)
From equations (1), (2), and (3), we obtain
∠DAC = ∠BCA = ∠BAC = ∠DCA ...(4)
⇒ ∠DCA = ∠BCA
Hence, AC bisects ∠C.
(ii) From equation (4), we obtain
∠DAC = ∠DCA
∴ DA = DC ...(Side opposite to equal angles are equal)
However, DA = BC and AB = CD ...(Opposite sides of a parallelogram)
∴ AB = BC = CD = DA
Hence, ABCD is a rhombus.
APPEARS IN
RELATED QUESTIONS
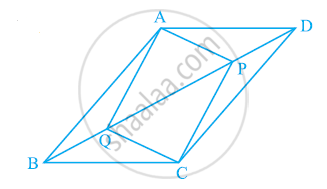
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
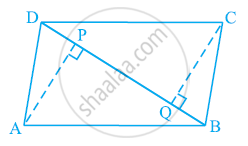
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.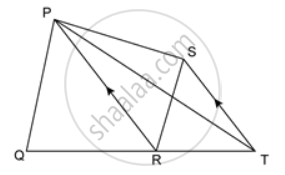
In the given figure, ABC is a triangle and AD is the median.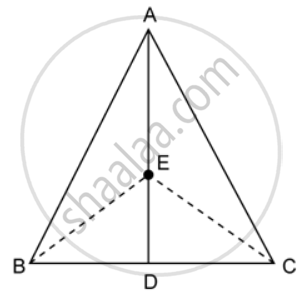
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of each of the following figure:
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
Give reason for the following :
Square is also a parallelogram.
