Advertisements
Advertisements
Question
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
Solution
The area of a square plot with side 80m
= 802
= 6400m2
Let the width of the rectangular plot = b
The area of a rectangle with length l and breadth b = A = l x b
The area of a rectangle wit length 160 and breadth b = A = 160 x b = 6400
⇒ b = `(6400)/(160)`
= 40m
The perimeter of a rectangle with length l and breadth b = P = 2(l + b)
The perimeter of a rectangle with length 160m and breadth 40m
= P
= 2(160 + 40)
= 2(200)
= 400m
The cost of fencing at the rate of Rs.7.50per m
= 400 x 7.50
= Rs.3000.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
In the given figure, ABC is a triangle and AD is the median.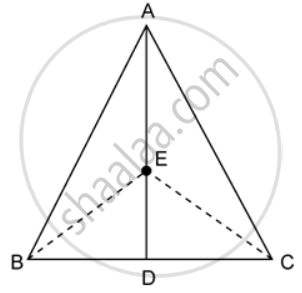
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Find the area of each of the following figure:
Find the area of each of the following figure: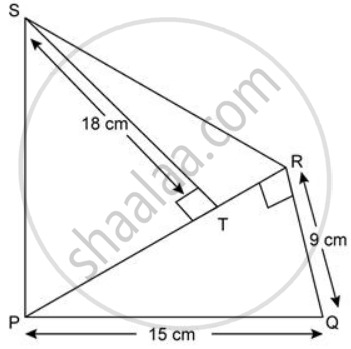
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Each angle of a rectangle is a right angle.
The diagonals of a square are perpendicular to one another.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Name polygon.

Make two more examples of this.
