Advertisements
Advertisements
Question
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
Options
True
False
Solution
True
Since a rhombus is a parallelogram, and we know that the diagonals of a parallelogram bisect each other, hence the diagonals of a rhombus too, bisect other.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
In the following figures, ABCD is a parallelogram.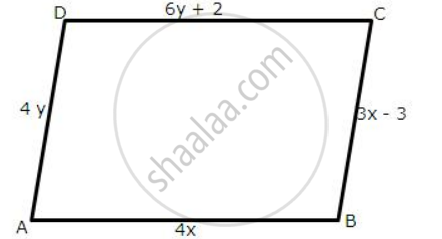
find the values of x and y.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.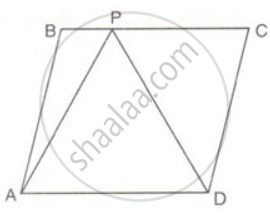
Prove that the median of a triangle divides it into two triangles of equal area.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, ABC is a triangle and AD is the median.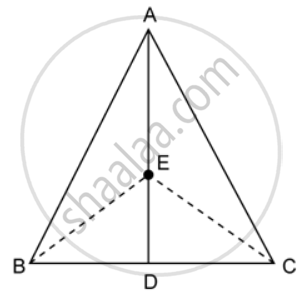
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
The opposite sides of a trapezium are parallel.
Examine whether the following is a polygon. If it is not, say why?

