Advertisements
Advertisements
Question
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
Solution
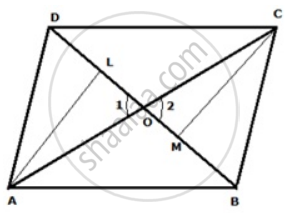
Join AC. Suppose AC and BD intersect at O. Draw AL and CM perpendicular to BD.
ar(ΔABD) = ar(ΔBDC)
Thus ΔABD and ΔABC are on the same base AB and have equal area.
Therefore, their corresponding altitudes are equal i.e. AL = CM.
Now,
In ΔALO and ΔCMO,
∠1 = ∠2 ...(vertically opposite angles)
∠ALO = ∠CMO ...(right angles)
AL = CM
Therefore,
ΔALO ≅ ΔCMO ...(AAS axiom)
⇒ AO = OC
⇒ BD bisects AC.
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show that the diagonals of a square are equal and bisect each other at right angles.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.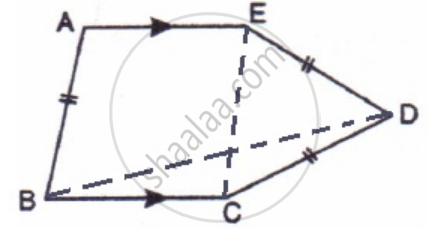
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN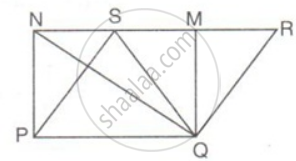
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.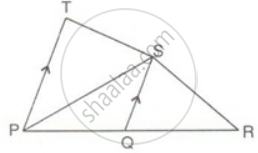
Prove that the median of a triangle divides it into two triangles of equal area.
In the given figure, ABC is a triangle and AD is the median.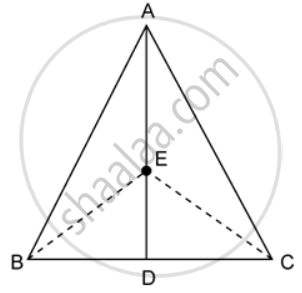
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
The opposite sides of a trapezium are parallel.
Give reason for the following :
Square is also a parallelogram.
Examine whether the following is a polygon. If it is not, say why?

