Advertisements
Advertisements
Question
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Solution
Area of rectangle ABCD = AB x AD = 7 x 25 = 175cm2
Area of triangle whose base is AB = `(1)/(2) xx "AB" xx "Height" = (1)/(2) xx 7 xx "Height"`
Now,
Area of triangle whose base is AB = 2 x Area of rectangle ABCD
⇒ `(1)/(2) xx 7 xx "Height"` = 175
⇒ Height
= `(175 xx 2)/(7)`
= 50cm.
APPEARS IN
RELATED QUESTIONS
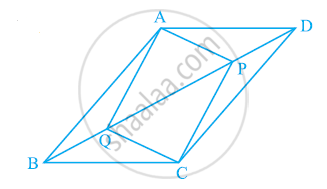
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.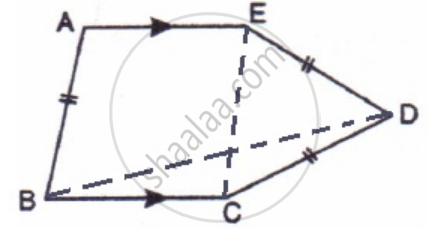
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.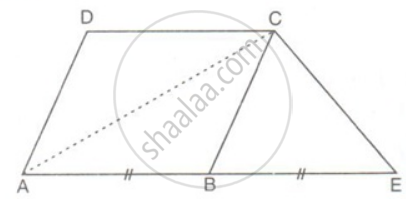
Prove that the median of a triangle divides it into two triangles of equal area.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
Find the area of each of the following figure:
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Examine whether the following is a polygon. If it is not, say why?

Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
