Advertisements
Advertisements
Question
Prove that the median of a triangle divides it into two triangles of equal area.
Solution
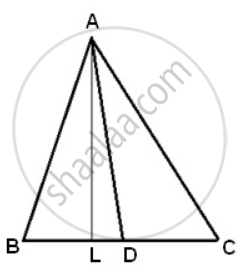
Draw AL perpendicular to BC.
Since AD is median of ΔABC. Therefore, D is the mid-point of BC.
⇒ BD = DC
⇒ BD x AL = DC x AL ...(multiplying by AL)
⇒ `(1)/(2)("BD" xx "AL")`
= `(1)/(2)("DC" xx "AL")`
⇒ ar(ΔABD) = ar(ΔADC).
APPEARS IN
RELATED QUESTIONS
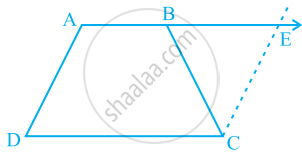
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.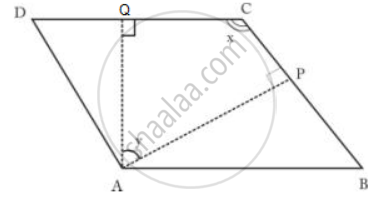
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the following figures, ABCD is a parallelogram.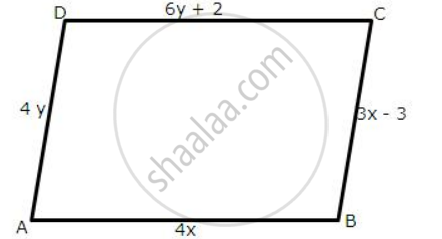
find the values of x and y.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.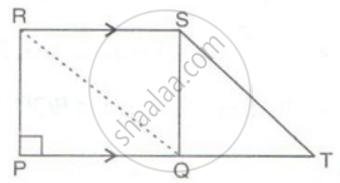
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Name polygon.

Make two more examples of this.
