Advertisements
Advertisements
Question
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.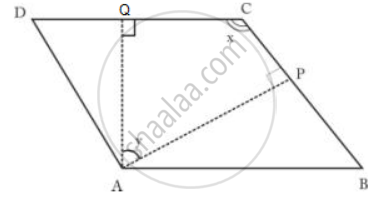
Solution
We know that AQCP is a quadrilateral. So sum of all angles must be 360.
∴ x + y + 90 + 90 = 360
x + y = 180
Given x : y = 2 : 1
So substitute x = 2y
3y = 180
y = 60
x = 120
We know that angle C = angle A = x = 120
Angle D = Angle B = 180 - x = 180 - 120 = 60
Hence, angles of a parallelogram are 120, 60, 120 and 60.
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.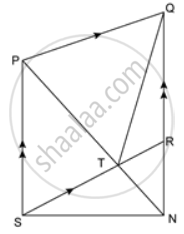
Prove that the median of a triangle divides it into two triangles of equal area.
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
The opposite sides of a rectangle are equal in length.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Square is also a parallelogram.
Name polygon.

Make two more examples of this.
