Advertisements
Advertisements
Question
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
Solution
Let us draw a parallelogram ABCD Where F is the midpoint Of side DC and E is the mid-point of side AB of a parallelogram ABCD.
To prove: AEFD is a parallelogram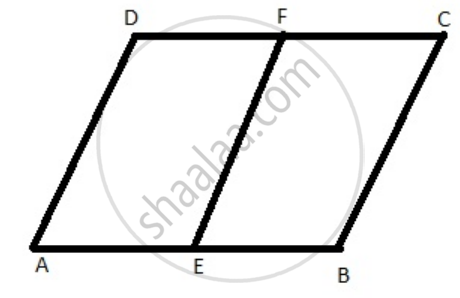
Proof:
In parallelogram ABCD
AB || DC
BC || AD
AB = DC
`1 /2"AB" = 1/2`DC
AE = DF
Also AD || EF
Therefore, AEFD is a parallelogram.
APPEARS IN
RELATED QUESTIONS
Prove that the bisectors of opposite angles of a parallelogram are parallel.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.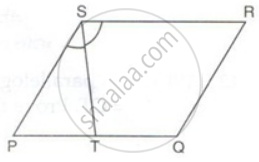
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.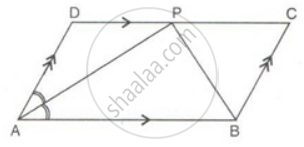
Prove that: ∠APB is a right angle.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.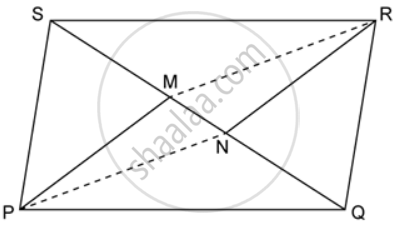
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.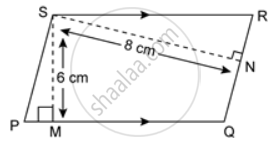
Find the perimeter of the parallelogram PQRS.

In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.