Advertisements
Advertisements
Question
Prove that the bisectors of opposite angles of a parallelogram are parallel.
Solution
Given ABCD is a parallelogram. The bisectors of ∠ADC and ∠BCD meet at E. The bisectors of ∠ABC and ∠BCD meet at F
From the parallelogram ABCD we have
∠ADC + ∠BCD = 180° ...[ sum of adjacent angles of a parallalogram ]
⇒ `("∠ADC")/(2) + ("∠BCD")/(2)` = 90°
⇒ ∠EDC + ∠EDC = 90°
In triangle ECD sum of angles = 180°
⇒ ∠EDC + ∠ECD + ∠CED = 180°
= ∠CED = 90°
Similarly taking triangle BCF it can prove that ∠BFC = 90°
Now since
∠BFC = ∠CED = 90°
Therefore the lines DE and BF are parallel
Hence proved
APPEARS IN
RELATED QUESTIONS
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.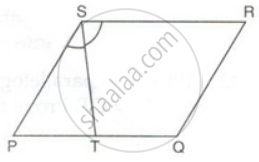
Prove that: RT bisects angle R
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.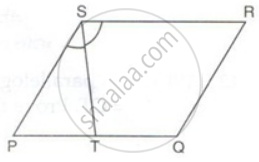
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.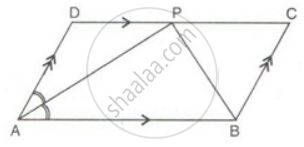
Prove that: BP bisects ∠ABC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.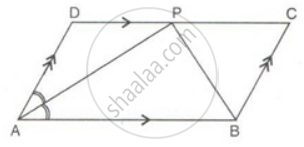
Prove that: ∠APB is a right angle.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.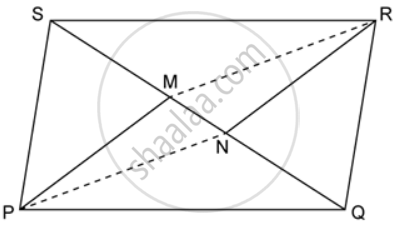
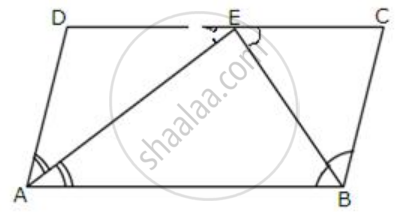
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
Find the perimeter of the parallelogram PQRS.

Which of the following statement is correct?
