Advertisements
Advertisements
प्रश्न
Prove that the bisectors of opposite angles of a parallelogram are parallel.
उत्तर
Given ABCD is a parallelogram. The bisectors of ∠ADC and ∠BCD meet at E. The bisectors of ∠ABC and ∠BCD meet at F
From the parallelogram ABCD we have
∠ADC + ∠BCD = 180° ...[ sum of adjacent angles of a parallalogram ]
⇒ `("∠ADC")/(2) + ("∠BCD")/(2)` = 90°
⇒ ∠EDC + ∠EDC = 90°
In triangle ECD sum of angles = 180°
⇒ ∠EDC + ∠ECD + ∠CED = 180°
= ∠CED = 90°
Similarly taking triangle BCF it can prove that ∠BFC = 90°
Now since
∠BFC = ∠CED = 90°
Therefore the lines DE and BF are parallel
Hence proved
APPEARS IN
संबंधित प्रश्न
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 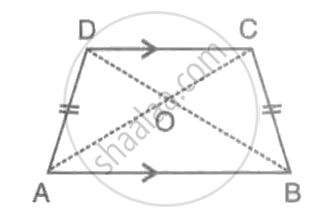
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.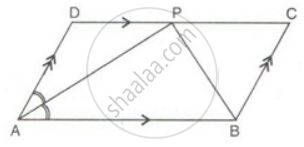
Prove that: BP bisects ∠ABC.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.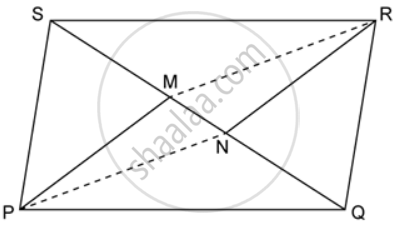
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.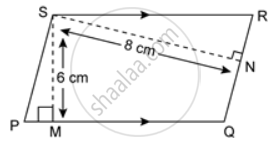
Find the perimeter of the parallelogram PQRS.

In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
