Advertisements
Advertisements
प्रश्न
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
उत्तर १
Points M are N taken on the diagonal AC of a parallelogram ABCD such that.
Prove that BMDN is a parallelogram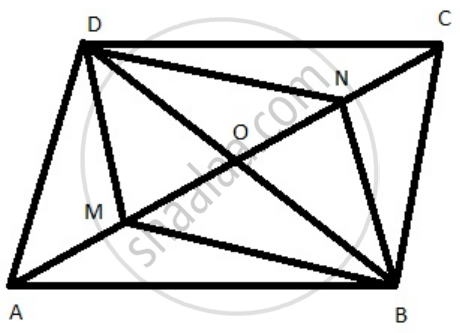
construction: Join B to D to meet AC in O.
Proof: We know that the diagonals of a parallelogram bisect each other.
Now, AC and BD bisect each other at O.
OC = OA
AM = CN
OA - AM = OC - CN
OM = ON
Thus in a quadrilateral BMDN, diagonal BD and MN are such that OM = ON and OD = OB
Therefore the diagonals AC and PQ bisect each other.
Hence BMDN is a parallelogram
उत्तर २
Join BD.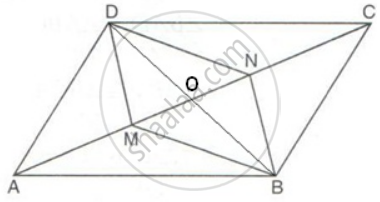
The diagonals of a parallelogram bisect each other.
Therefore, AC and BD bisect each other.
⇒ OA = OC
But AM = CN
Therefore,OA - AM = OC - CN
⇒ OM = ON
Therefore, in quadrilateral BMDN,
OM = ON and OD = OB
⇒ Diagonals MN and BD bisect each other
⇒ BMDN is a parallelogram.
संबंधित प्रश्न
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
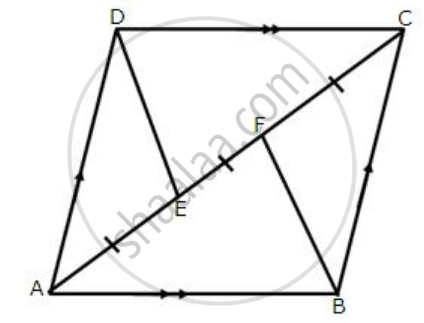
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
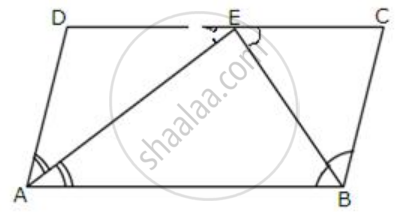
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.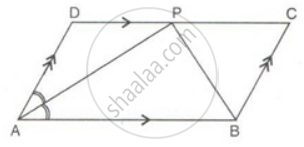
Prove that: ∠APB is a right angle.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.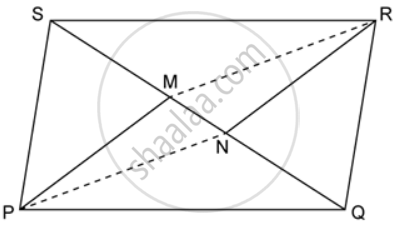
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
Find the perimeter of the parallelogram PQRS.

In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD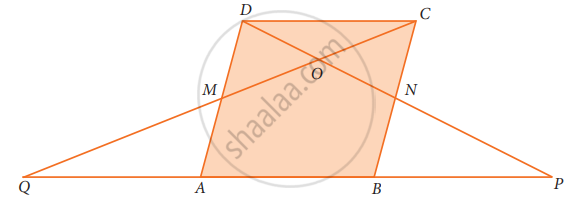
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?