Advertisements
Advertisements
Question
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
Solution 1
Points M are N taken on the diagonal AC of a parallelogram ABCD such that.
Prove that BMDN is a parallelogram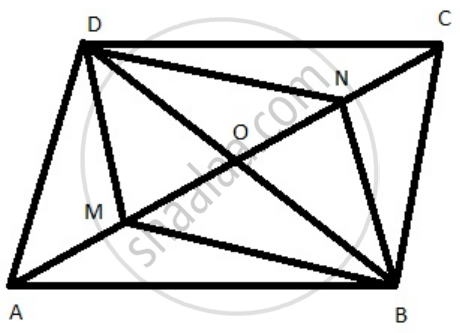
construction: Join B to D to meet AC in O.
Proof: We know that the diagonals of a parallelogram bisect each other.
Now, AC and BD bisect each other at O.
OC = OA
AM = CN
OA - AM = OC - CN
OM = ON
Thus in a quadrilateral BMDN, diagonal BD and MN are such that OM = ON and OD = OB
Therefore the diagonals AC and PQ bisect each other.
Hence BMDN is a parallelogram
Solution 2
Join BD.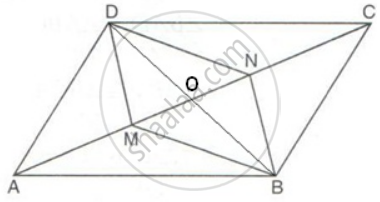
The diagonals of a parallelogram bisect each other.
Therefore, AC and BD bisect each other.
⇒ OA = OC
But AM = CN
Therefore,OA - AM = OC - CN
⇒ OM = ON
Therefore, in quadrilateral BMDN,
OM = ON and OD = OB
⇒ Diagonals MN and BD bisect each other
⇒ BMDN is a parallelogram.
APPEARS IN
RELATED QUESTIONS
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
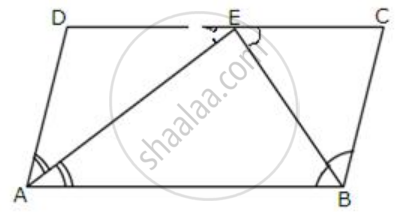
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
Prove that the bisectors of opposite angles of a parallelogram are parallel.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.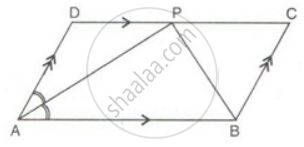
Prove that: BP bisects ∠ABC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.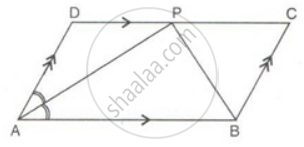
Prove that: ∠APB is a right angle.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
Find the perimeter of the parallelogram PQRS.

In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
