Advertisements
Advertisements
Question
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
Solution
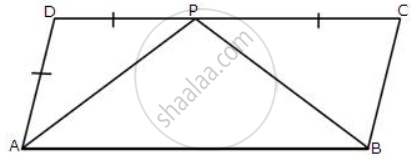
Consider ΔADP and ΔBCP,
AD = BC ....[ Since ABCD is a parallelogram. ]
DC = AB ....[ Since ABCD is a parallelogram. ]
∠A ≅ ∠C ....[ Opposite angles ]
ΔADP ≅ ΔBCP .....[ SAS ]
Therefore, AP = BP
AP bisects ∠A
BP bisects ∠B
In ΔAPB, AP = BP
AP bisects ∠A
BP bisects ∠B
In ΔAPB,
AP = PB
∠APB = ∠DAP + ∠BCP
Hence proved
APPEARS IN
RELATED QUESTIONS
In a parallelogram `square`ABCD, If ∠A = (3x + 12)°, ∠B = (2x - 32)° then find the value of x and then find the measures of ∠C and ∠D.
In the following figures, find the remaining angles of the parallelogram
In the following figures, find the remaining angles of the parallelogram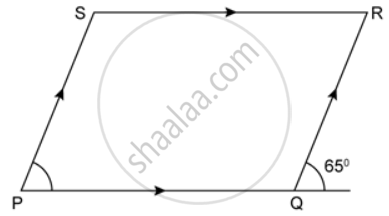
In a parallelogram ABCD ∠C = 98°. Find ∠A and ∠B.
Find the measures of all the angles of the parallelogram shown in the figure: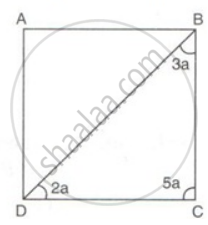
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
The sum of adjacent angles of a parallelogram is ______.
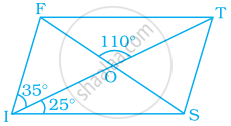
In parallelogram FIST, find ∠SFT, ∠OST and ∠STO.
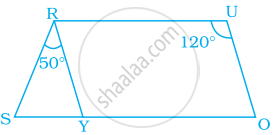
In the given parallelogram YOUR, ∠RUO = 120° and OY is extended to point S such that ∠SRY = 50°. Find ∠YSR.