Advertisements
Advertisements
प्रश्न
In the following figure, ABCD is a parallelogram. 
Prove that:
(i) AP bisects angle A.
(ii) BP bisects angle B
(iii) ∠DAP + ∠BCP = ∠APB
उत्तर
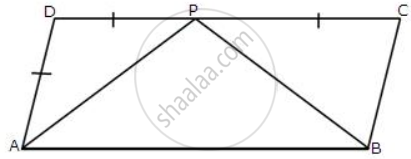
Consider ΔADP and ΔBCP,
AD = BC ....[ Since ABCD is a parallelogram. ]
DC = AB ....[ Since ABCD is a parallelogram. ]
∠A ≅ ∠C ....[ Opposite angles ]
ΔADP ≅ ΔBCP .....[ SAS ]
Therefore, AP = BP
AP bisects ∠A
BP bisects ∠B
In ΔAPB, AP = BP
AP bisects ∠A
BP bisects ∠B
In ΔAPB,
AP = PB
∠APB = ∠DAP + ∠BCP
Hence proved
APPEARS IN
संबंधित प्रश्न
In the following figures, find the remaining angles of the parallelogram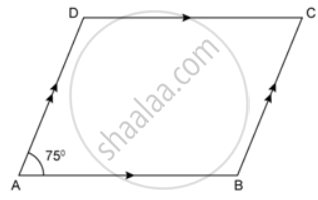
In the following figures, find the remaining angles of the parallelogram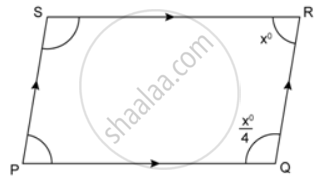
In the following figures, find the remaining angles of the parallelogram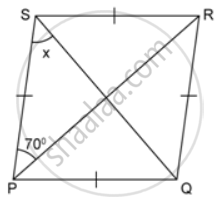
In a parallelogram ABCD ∠C = 98°. Find ∠A and ∠B.
Find the measures of all the angles of the parallelogram shown in the figure: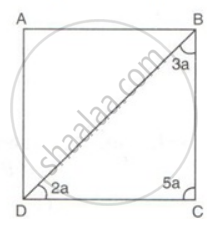
The angles of a triangle formed by 2 adjacent sides and a diagonal of a parallelogram are in the ratio 1 : 5 : 3. Calculate the measures of all the angles of the parallelogram.
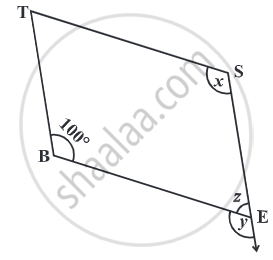
Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD.
If PQRS is a parallelogram, then ∠P – ∠R is equal to ______.
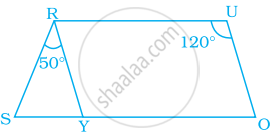
In the given parallelogram YOUR, ∠RUO = 120° and OY is extended to point S such that ∠SRY = 50°. Find ∠YSR.