Question

ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;

prove that AP and DQ are perpendicular to each other.

Answer 1

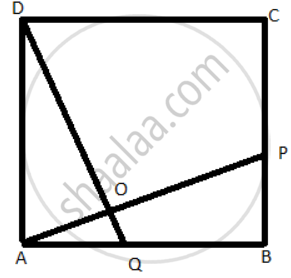
ABCD is a square and AP = PQ

Consider ΔDAQ and ΔABP,

∠DAQ = ∠ABP = 90°

DQ = AP 

AD = AB

ΔDAQ ≅ ΔABP

⇒ ∠PAB = ∠QDA

Now,

∠PAB + ∠APB = 90°

also ∠QDA + ∠APB = 90°      ...[∠PAB = ∠QDA]

Consider ΔAOQ by ASP

∠QDA + ∠APB + ∠AOD = 180° 

⇒ 90° + ∠AOD = 180° 

⇒ ∠AOD = 90° 

Hence, AP and DQ are perpendicular.