Advertisements
Advertisements
प्रश्न
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
उत्तर
Construction: Join QR. Let the diagonals PR and QS intersect each other at point O.
Since diagonals of a parallelogram bisect each other, therefore O is the mid-point of both PR and QS.
Now, median of a triangle divides it into two triangles of equal area.
In ΔPSQ, OP is the median.
∴ Area(ΔPOS) = Area(ΔPOQ) ….(i)
Similarly, OT is the median of ΔTSQ.
∴Area(ΔTOS) = Area(ΔTOQ) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔPOS) - Area(ΔTOS) = Area(ΔPOQ) - Area(ΔTOQ)
⇒ Area(ΔPTQ) = Area(ΔPTS)
⇒ Area(ΔPTS) = 18 square units.
APPEARS IN
संबंधित प्रश्न
Identify all the quadrilaterals that have four right angles
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
Explain how a square is a rhombus.
Explain how a square is a rectangle
Prove that the bisectors of the interior angles of a rectangle form a square.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;
prove that AP and DQ are perpendicular to each other.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.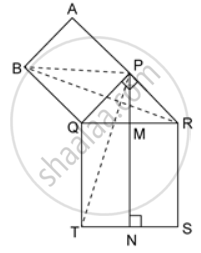
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
