Advertisements
Advertisements
प्रश्न
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
उत्तर
Construction: Join SM and SQ.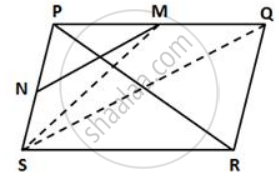
In a parallelogram PQRS, SQ is the diagonal.
So, it bisects the parallelogram.
∴ Area(DPSQ) = `(1)/(2) xx "Area(parallelogram PQRS)"`
SM is the median of ΔPSQ.
∴ Area(ΔPSM) = `(1)/(2) xx "Area(ΔPSQ)"`
= `(1)/(2) xx (1)/(2) xx "Area(parallelogram PQRS)"`
= `(1)/(4) xx "Area(parallelogram PQRS)"`
Again, MN is the median of ΔPSM.
∴ Area(ΔPMN) = `(1)/(2) xx "Area(ΔPSM)"`
= `(1)/(2) xx (1)/(4) xx "Area(parallelogram PQRS)"`
= `(1)/(8) xx "Area(parallelogram PQRS)"`
⇒ 20 = `(1)/(8) xx "Area(parallelogram PQRS)"`
⇒ Area(parallelogram PQRS) = 160 square units.
APPEARS IN
संबंधित प्रश्न
All rectangles are squares
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Identify all the quadrilaterals that have four right angles
Explain how a square is a rectangle
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.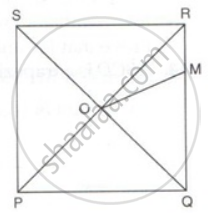
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
