Advertisements
Advertisements
Question
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
Solution
Construction: Join SM and SQ.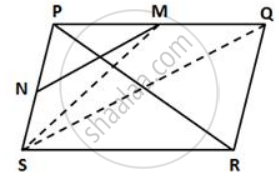
In a parallelogram PQRS, SQ is the diagonal.
So, it bisects the parallelogram.
∴ Area(DPSQ) = `(1)/(2) xx "Area(parallelogram PQRS)"`
SM is the median of ΔPSQ.
∴ Area(ΔPSM) = `(1)/(2) xx "Area(ΔPSQ)"`
= `(1)/(2) xx (1)/(2) xx "Area(parallelogram PQRS)"`
= `(1)/(4) xx "Area(parallelogram PQRS)"`
Again, MN is the median of ΔPSM.
∴ Area(ΔPMN) = `(1)/(2) xx "Area(ΔPSM)"`
= `(1)/(2) xx (1)/(4) xx "Area(parallelogram PQRS)"`
= `(1)/(8) xx "Area(parallelogram PQRS)"`
⇒ 20 = `(1)/(8) xx "Area(parallelogram PQRS)"`
⇒ Area(parallelogram PQRS) = 160 square units.
APPEARS IN
RELATED QUESTIONS
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Explain how a square is a rhombus.
Explain how a square is a rectangle
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
Prove that the bisectors of the interior angles of a rectangle form a square.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.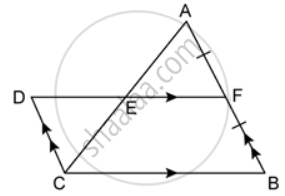
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
