Advertisements
Advertisements
Question
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
Solution
Construction: Join QR. Let the diagonals PR and QS intersect each other at point O.
Since diagonals of a parallelogram bisect each other, therefore O is the mid-point of both PR and QS.
Now, median of a triangle divides it into two triangles of equal area.
In ΔPSQ, OP is the median.
∴ Area(ΔPOS) = Area(ΔPOQ) ….(i)
Similarly, OT is the median of ΔTSQ.
∴Area(ΔTOS) = Area(ΔTOQ) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔPOS) - Area(ΔTOS) = Area(ΔPOQ) - Area(ΔTOQ)
⇒ Area(ΔPTQ) = Area(ΔPTS)
⇒ Area(ΔPTS) = 18 square units.
APPEARS IN
RELATED QUESTIONS
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
Explain how a square is a rectangle
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.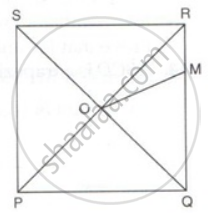
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.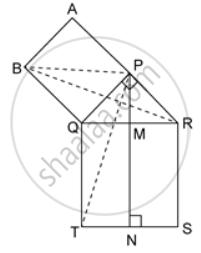
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.