Advertisements
Advertisements
Question
All squares are rhombuses and also rectangles.
Options
True
False
Solution
This statement is True.
Explanation:
All squares are rhombuses as all sides of a square are of equal lengths. All squares are also rectangles as each internal angle measures 90°
APPEARS IN
RELATED QUESTIONS
All rectangles are squares
Explain how a square is a quadrilateral
Explain how a square is a parallelogram
Explain how a square is a rhombus.
In a quadrilateral ABCD, AB = AD and CB = CD.
Prove that:
- AC bisects angle BAD.
- AC is the perpendicular bisector of BD.
Prove that the bisectors of the interior angles of a rectangle form a square.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.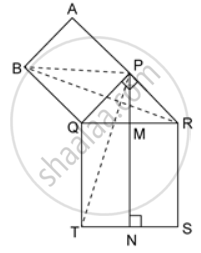
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
